Baumdiagramme und zweistufige Zufallsexperimente
Klaras Kleiderschrank
In Klaras Kleiderschrank liegen vier Tops (T) und drei Röcke (R). Welche Möglichkeiten hat Klara, die Tops und Röcke zu kombinieren?
Sie kann jeden der drei Röcke (R1, R2, R3) jeweils mit einem der vier Tops (T1, T2, T3, T4) zusammen anziehen. Das können wir auch so veranschaulichen:
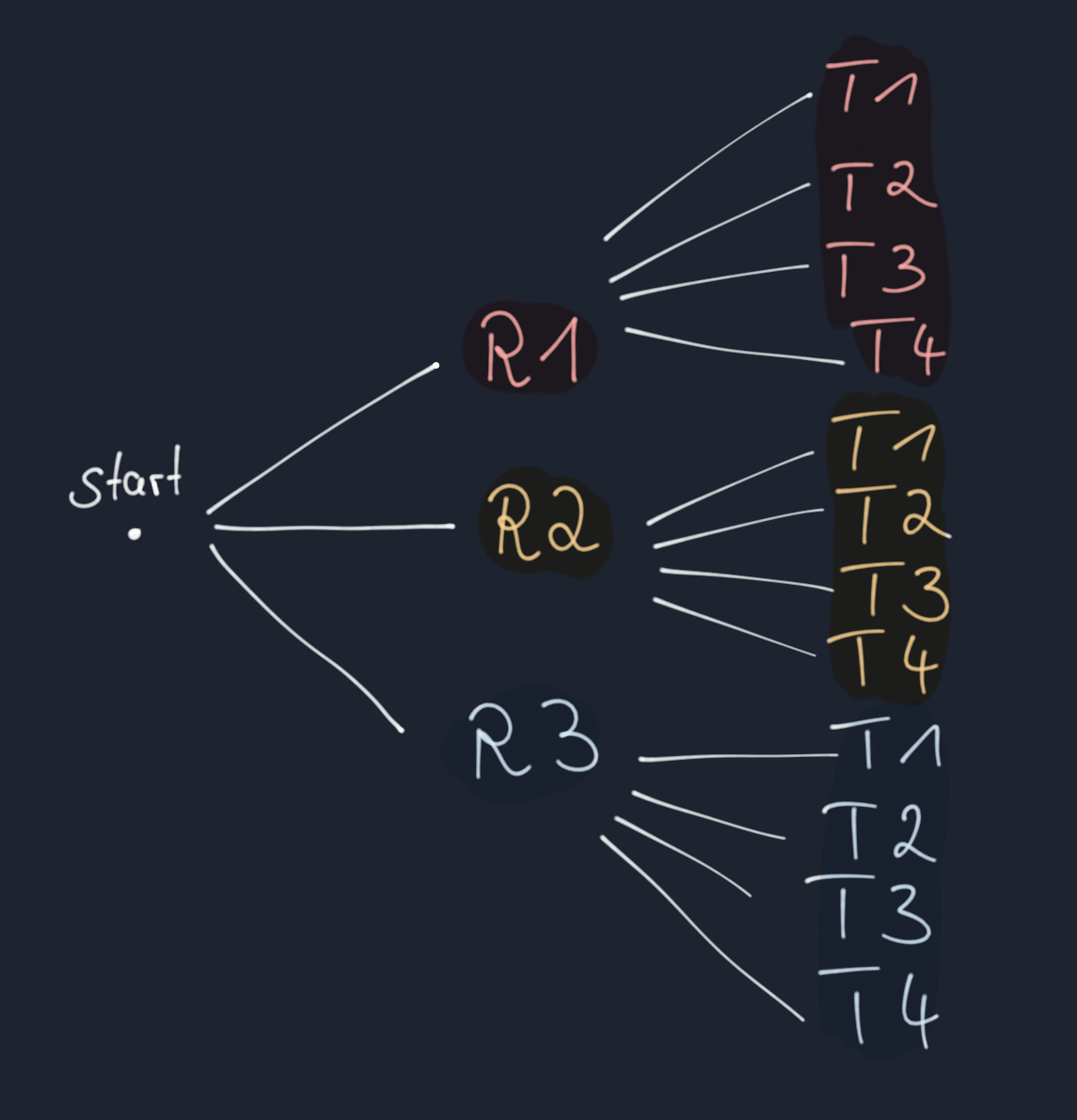
Damit ergeben sich insgesamt 12 Kombinationen.
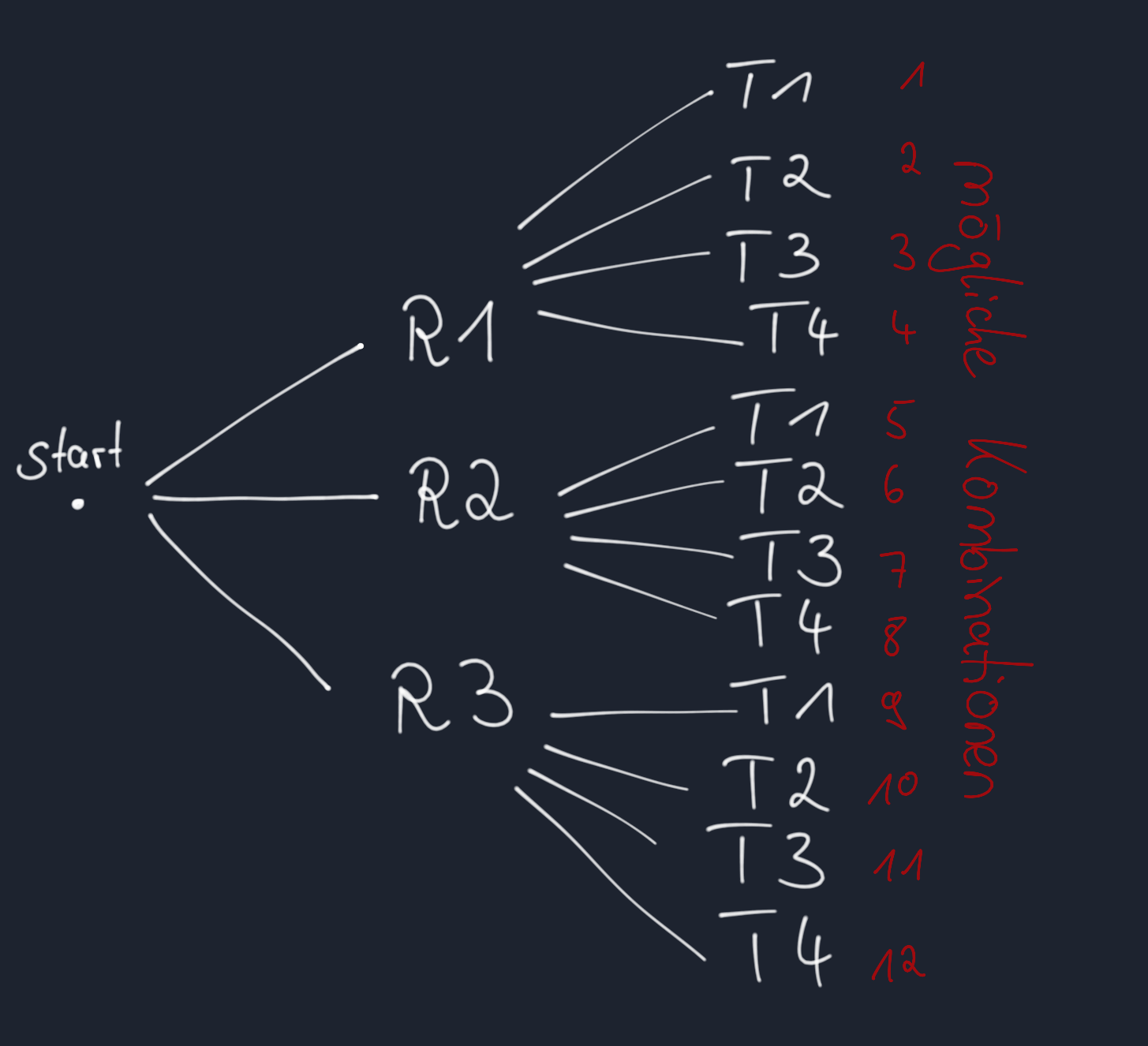
Eine solche Darstellung nennt man Baumdiagramm.
Definition mehrstufige Zufallsexperimente
Mehrstufige Zufallsexperimente, sind Zufallsexperimente, die aus einzelnen hintereinander ausgeführten Zufallsexperimenten bestehen.
Bemerkung mehrstufige Zufallsexperimente
Dabei kann so ein mehrstufiges Zufallsexperiment entweder aus unterschiedlichen Zufallsexperimenten bestehen, wie im Kleiderschrankbeispiel, bei dem erst aus Röcken und dann aus Tops ausgewählt werden sollte, oder eine Wiederholung des gleichen Experiments sein, zum Beispiel beim zweimaligem Würfeln.
Baumdiagramm
Für sogenannte mehrstufige Zufallsexperimente bietet es sich an, die möglichen Ergebnisse in einem Baumdiagramm zu strukturieren. Dazu wird auf die linke Seite zuerst ein Startpunkt markiert (entweder doch einen Punkt oder das Wort "start"). Danach werden von da aus alle einzelnen Ergebnisse des ersten Experiments aufgelistet und mit dem Startpunkt verbunden. Nun betrachten wird von jedem Ergebnis des ersten Experiments immer eine Verbindung zu allen Ergebnissen des zweiten Experiments gezogen, da man erstmal davon ausgeht, dass nach jedem der ersten Ergebnisse immer jedes der zweiten Ergebnisse auftreten kann
Was heißt das jetzt?
Angenommen für unser erstes Experiment ΩA ist die Ergebnismenge
ΩA = {A1, A2, A3}
und für unser zweites Experiment ΩB die Ergebnismenge
ΩB = {B1, B2}.
Dann kann nach jedem A eins der B's folgen, also ergibt sich folgendes Baumdiagramm:
BILD
abzählen der Pfade
Einen Weg vom Startpunkt bis zu einem beliebigen der Endpunkte im Baumdiagram bezeichnet man als Pfad. Zählt man alle Pfade bzw. Endpunkte zusammen, so erhält man die Anzahl der Möglichkeiten eines mehrstufigen Zufallsexperiments.
Wahrscheinlichkeiten in Baumdiagrammen
Notation der Wahrscheinlichkeiten
Auch Wahrscheinlichkeiten finden ein einem solchen Baumdiagramm platz! So werden die Wahrscheinlichkeiten eines einzelnen Ergebnisses immer auf den Strich der zu dem Ergebnis führt notiert. Aber auch die Wahrscheinlichkeit eines gesamten Pfads kann man bestimmen. Wie das geht sehen wir später noch. Diese wird dann am Ende des Pfads notiert.
Produktregel
Summenregel
Urnenmodell
Ziehen mit Zurücklegen
Ziehen ohne Zurücklegen
